wher 101;&#EМлад модул,-Iинерционният момент на диаметралната част на шахтата,-к initNameмх Двест8111; коефициент на твърдост на момента на еквивалентна връзка, съответстваща на напълно отворена пукнатина. Уравнението има две сумманди; гъвкавост, свързана с пукнатината и гъвкавостта на лъча без пукнатина.Да.

 Трябва да се отбележи, че независимо от формата на лъча, условията на границите и положението на пукнатината приносът към общата гъвкавост на лъча зависи само от коефициента к initNameмт Не.т.е. първият сумманд. Докато лъчът се върти, гъвкавостта в пукнатината се променя.Ние получаваме следното:wher 101; 

 пр о&#гъвкавостта на лъча без пукнатина;  qName=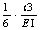 -кмхтекущия коефициент на якост на дадения моментqДобре. -Включвайки две уравнения (5) и (7), получаваме:wher101;като вземем предвид уравнението (6) получаваме закона за промяната на твърдостта на момента в зависимост от разликата в фазите.

 е q 

 Да.Получената якост на еквивалентна връзка зависи само от диаметъра на шахтата, характеристиките на материала и дълбочината на пукнатината.Промяна в положението на пукнатина в шахтата, характеристиките на шахтата, включително опорните възли, не променят твърдостта на момента на еквивалентна връзка (при&#при условие че частта с пукнатината остава същата във всяка част на частта с пукнатината, за която е билаполучава).Връщайки се към матрицата на сковаността, получена преди, нейните коефициенти на твърдост могат да бъдат записани по следния начин: wher 

101; к

initName 

 о Не. к  initName 

 Ааа! начални стойности на твърдостта на момента при съответните оси за напълно отворена пукнатина&#Добре. Задачата на кinitName оНе.кinitName  -Ааа!изчислението може да се реши по два начина.Първият е изчисляване на твърдостта на момента в програмата FEM.Втората е да се използва теорията за механиката на фрактурите.Тя дава възможност да се изчислят стойностите на коефициентите на локална гъвкавост на откритата пукнатина, ако геометрията, диаметъра на шахтата и характеристиките на материала са известни [7,10].

 Алгоритъм за симулиране на роторна система с пукнатина Следва да се преминат следните стъпки, за да се получат коефициенти на якост на пукнатината.1. В една от специализираните програми се създава пълният ротор модел за анализ на динамиката на ротора (занапример в динамични R4).2. Отрядът на ротора с пукнатина е подчертан.  3. Пукнатината разделя шахтата на две подсистеми.Връзка, описана от матрицата на променливатаКоефициенти на твърдост[К (q 

 Не. 

й]

от

измерението 6x6 се поставя между подсистемите.

4. Начални коефициенти на твърдост на момента

к

initName

о Не.кinitNameАаа!за открита пукнатина се получават чрез дадените методинад.Тези данни са първоначални за изчисляване.Стойностите на матричната матрица на връзката, симулираща пукнатина, се изчисляват при интегриране на уравненията за движение. 

на роторната система за всекиqДобре.При нелинейна матрична формула, описваща нелинейния динамичен моделна роторната система е следната: wher101;[М Не.

общо 8211; матрица на инерционните коефициенти;

 [ В Не.

общо 8211; матрица на коефициентите на овлажняване и жироскоп;[К

Не. 

 матрица на коефициенти на твърдост; Не.&#о}Не.Не.о}Не.Не.о}заделени 8211; колони с вибрационни ускорения, вибрационни скорости и вибрационни измествания съответно;Не.-F(ит)тName}&&всеки Видове динамични натоварвания в рамките на задгранични зони, вътрешни и външни.Стифнес матрицата на еквивалентна връзка може да бъде разделена на две части: постоянна и променлива, и това е вярно:[&К В] е включен в общата матрица на твърдостта на[КНе.система.Матрица() [q j] nНе.Ксе използва за изчисляванереакции на нелинейна връзка:-wher101; 

 о rx Не. 

 о реamount in units (real)всъщност завъртания на секциите около съответните оси.Окончателното уравнение на движението на системата е следното:Да.Даденото уравнение може да се реши чрез цифрови методи като RungeМетод Kutta, метод Newmark, и т.н.Приложимостта на предложения алгоритъм се извършва чрез сравнение на гъвкавостта на дветеносещ лъч спукнатина, получена в краенЕлементна система и според предполагаемия алгоритъм в динамични R4.Задачата е да се изчисли деформацията на лъча под единица сила в разделителните части за различните фази между пукнатината и силата.Фигура 3 показва резултатите от проверката на предложения алгоритъм.Сравняват се три резултата:гъвкавостта се изчислява по метода на фините елементи (FEM).Радиалната гъвкавост на модела на лъча с пукнатина се изчислява в FEM

система за целия диапазон от ъглови позиции на пукнатината;&#гъвкавостта се изчислява с помощта на Dynamics R4, първоначалните данни се получават чрез FEM.Начални стойности на моментаскованост за напълно отворена пукнатинак initNameоНе. кinitName

Ааа!са получени уравнения за решаване (7) за

к-initName

мх-и радиална гъвкавост на лъча с пукнатина

gc-в съответната посока се изчислява чрез FEM.Моментната скованост за междинните ъглови позиции на пукнатината се променя от минимум на максимум съгласно (10) закона;

гъвкавостта се изчислява с помощта на Dynamics R4.Първоначални данни за гъвкавостта на момента за напълно открита пукнатина

-к-о

 initName Не. к-Ааа!  

initNameсе получават аналитично чрез алгоритмите на механиката на фрактурите [7, 10].Стойност на гъвкавостта на момента замеждинните ъглови позиции на пукнатината се променят от минимум към максимум съгласно закона (10).Фигура 3 Промяна в гъвкавостта на лъча в раздела на пукнатините за една революция Резултатите при изчисляването на FEMмодел и модели в динамични R4 са близки.Резултатите от изчисленията при първоначално получени аналитично условия се различават от резултатите от FEM по-малко от 1%.В същото време първоначалната скованост се изчислява аналитично много по-бързо от изчисляването на FEM и изисква по-малко работно време и по-лесно.доупотреба.  Геометрия и параметри на ротора с пукнатина Геометрията на ротора с пукнатина се избира, за да се покаже работата на алгоритъма с най-голямо предимство, таблица 1.ротор с централния диск, опорите се поставят на краищата на шахтата.② ②②②

 ② ②-②②②②②②②②②  ② 

②

 ② ② ②-②-②-② 

②

 ② ② ②